altataya.blogg.se - Unit circle formulas all students take calculus

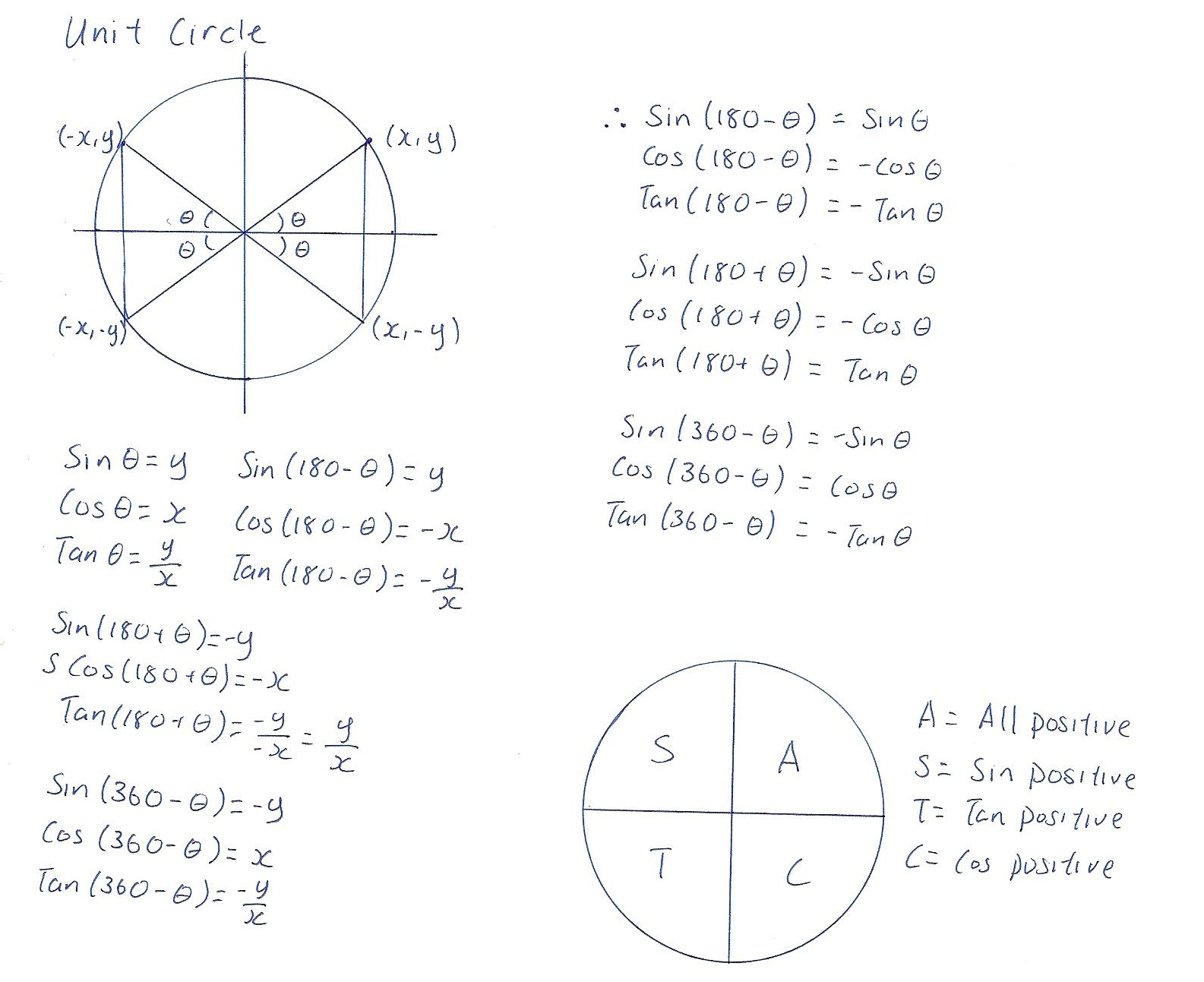
These ratios can be simplified a bit because you are constrained to working on the unit circle: These will always be positive numbers, because the length of any side is positive (by the Ruler Postulate).

tan A = a/ b, sin A = a/ c, and cos A = b/ c.

Whenever you talk about A, you should always refer to BAC, an interior angle of your triangle. Notice that the orientation of the right triangle changes, but the hypotenuse is always the line segment ¯AB.įigure 20.10 Four right triangles embedded in the unit circle, based on the location of the vertex B. In Figure 20.10, I've shown four different locations for B and the corresponding embedded right triangles that result. Now, let B move around the circle and always embed a right triangle by dropping a perpendicular line segment from B to ¯XY. That's the advantage of working on the unit circle. You can't have a nicer denominator of a ratio than 1. Recall that the sine and cosine ratios both involve the length of the hypotenuse in the denominator.

Because you are working with the unit circle, your hypotenuse has length 1. The hypotenuse of your triangle has one end point located at the center of the circle and the other end point on the circle. Keep the diameter that C lies on fixed (in this case, ¯XY), and let B move around the circle. The only nice property left is the triangle's right angle, so by process of elimination C is the right angle. It can move around the circle and occupy whatever place it wants, but it must stay on the circle. Think of vertex A as being in a trigonometric “time out.” Vertex B is constrained to lie on the circle. It is not allowed to move from that point. Keep vertex A at the center of the circle.

Use Figure 20.9 as a guide.įigure 20.9 A right triangle embedded in the unit circle.Įach one of the vertices of the triangle will have some special characteristic, but the coveted properties are spread around so that one vertex isn't seen as being “better” than any other. Let's embed a right triangle into a unit circle and see what happens. Well, the unit circle is a circle with radius equal to 1. Although you could use any circle, things work out nicely if you use the “unit circle.” You might be wondering what the unit circle is and why you should use that particular circle. But in order to do this, you must embed a right triangle into a circle. The sine, cosine, and tangent ratios can be defined for any angle, not just acute angles. So you can only find the trigonometric ratios of acute angles. Because the measures of the interior angles of a right triangle add up to 180º, and one of these angles has a measure equal to 90º, the other two angles of a right triangle must be acute angles. Our trigonometric ratios were defined within the confines of a right triangle. How Does This Relate to the Unit Circle?.